第二届“华罗庚金杯”少年数学邀请赛初赛答案

第二届“华罗庚金杯”少年数学邀请赛初赛答案

1.第八届　　2．11　　3．121　　4．1981　　5．58%　　6．0　　7．13.42　　8．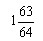 　

9．第三个　　10．3点钟　　11．13　　12．36人　　13．第十次交换座位后，小兔坐在第2号位子

14．能排成4个被11除余8的数　　15．100个

1．【解】“每隔一年举行一次”的意思是每两年举行1次。1988年到2000年还有2000－1988＝12年，因此还要举行12÷2＝6届。1988年是第二届，所以2000年是1＋6＝8届。

这题目因为数字不大，直接数也能很快数出来：1988、1990、1992、1994、1996、1998、2000年分别是第二、三、四、五、六、七、八届．

答：2000年举行第八届．

【注】实际上，第三届在1991年举行的，所以2001年是第八届.

2．【解】由于两只蚂蚁的速度相同，所以大、小圆上的蚂蚁爬一圈的时间的比应该等于圈长的比．而圈长的比又等于半径的比，即：33∶9．

　要问两只蚂蚁第一次相遇时小圆上的蚂蚁爬了几圈，就是要找一个最小的时间它是大、小圆上蚂蚁各自爬行一圈所需时间的整数倍．适当地选取时间单位，使小圆上的蚂蚁爬一圈用9个单位的时间，而大圆上的蚂蚁爬一圈用33个单位的时间．这样一来，问题就化为求9和33的最小公倍数的问题了．不难算出9和33的最小公倍数是99，所以答案为99÷9=11．

答：小圆上的蚂蚁爬了11圈后，再次碰到大圆上的蚂蚁．

 

更多内容请下载：第二届“华罗庚金杯”少年数学邀请赛初赛答案

第二届“华罗庚金杯”少年数学邀请赛初赛